
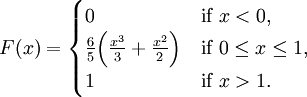

#Find cdf from pdf pdf
Now, the height of the PDF is 1 over the area of S. So the total volume sitting on top of this little set is going to be the base, the area of the base, which is the area of A intersection S times the height of the PDF at those places. So the relevant area is only this part here, which is the intersection of the two sets, S and A. Well, actually, the PDF is 0 outside the set S. To calculate the probability of a certain set A, we want to ask how much volume is sitting on top of that set.Īnd because in this case, the PDF is constant, we need to take the height of the PDF times the relevant area. So the overall probability, one unit of probability, is spread uniformly over that set.īecause the total volume under the joint PDF must be equal to 1, the height of the PDF must be equal to 1 over the area. The simplest kind of a joint PDF is a PDF of that is constant on a certain set, S, and is 0 outside that set.
#Find cdf from pdf plus
It is an integral with respect to the second variable.Īnd it's an integral over the entire space, from minus infinity to plus infinity. And when we have an integral of this kind and we differentiate with respect to the upper limit of the integration, what we are left with is the integrand. Now, to find the density of X, all we need to do is to differentiate the CDF of X. Think of this double integral as an integral with respect to the variable s of this complicated function inside the brackets. So it ranges from minus infinity to infinity.īut the variable s, the first argument, ranges from minus infinity up to this point, which is x. Now, since we've used the symbol x here to mean something specific, let us use different symbols for the dummy variables that we will use in the integration.Īnd we need to integrate with respect to the two variables, let's say with respect to t and with respect to s.

So it will be a double integral of the joint density over this particular two-dimensional set. So we need to integrate over this two-dimensional set the joint density. If here is the value of little x, then we're talking about the set of all pairs x, y, for which the x component is less than or equal to a certain number. The CDF of X is, by definition, the probability that the random variable X takes a value less than or equal to a certain number little x.Īnd this is the probability of a particular set that we can visualize on the two dimensional plane. So let us start by first finding the CDF of X. Replace sums by integrals, and replace PMFs by PDFs.īut a proof of this formula is actually instructive. You can easily guess the formula through the standard recipe. Things are similar in the continuous setting. It is their probability law, and any quantity of interest can be computed if we know the joint. Indeed, the joint PMF is supposed to contain a complete probabilistic description of the two random variables. In the discrete case, we saw that we could recover the PMF of X and the PMF of Y from the joint PMF.


 0 kommentar(er)
0 kommentar(er)
